Plotting
Tracciamento del diagramma di funzioni
>> x=linspace(0,100,512); >> plot(x,sqrt(x))
Mostra il diagramma
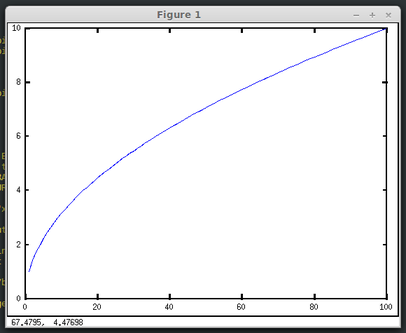
Ma la funzione plot può tracciare più di una funzione alla volta
>> x=linspace(0,2*pi,100)'; >> s=[sin(x) sin(2*x) sin(3*x) cos(x) cos(2*x) cos(3*x)]; >> plot(x,s)
Notare che linspace
viene trasposta con l'operatore
x
in un vettore. Quindi le funzioni sin
sono
tutti vettori e vanno a comporre una matrice, la funzione
plot lavora per colonne
e traccia la tutte le colonne
della matrice s
xm=[cos(3*x+alfa) cos(x+alfa) cos(2*x+alfa)... sin(3*x+alfa) sin(x+alfa) sin(2*x+alfa)]scegliendo un valore per alfa tracciate
plot(xm,s)Il risultato sono alcune figure di Lissajou.
Plot 3D
Il plot in 3 dimensioni richiede che si costruisca un dataset costituito da terne di coordinate nello spazio cartesiano 3-dimensionale.
Il tracciamento di superfici è un caso importante di plot 3D nella nostra prospettiva perchè un immagine è costruita da punti luminosi (pixel) rappresentati secondo il modello RGB o grayscale . Un immagine è quindi una sorta di rappresentazione del valore di una funzione che dipende dalle coordinate dei pixel (u,v) dell'immagine.
In analogia a quanto mostrato per il caso del diagramma 2-D costruiamo delle superfici d'esempio a partire da espressioni analitiche per poter chiarire il ruolo delle funzioni che intervengono nel plotting 3-dimensionale
Le operazioni necessarie sono nella costruzione di 2 matrici con la funzione meshgrid
- La prima contiene il valore di X per ogni punto da tracciare
- La seconda contiene il valore di Y per ogni punto da tracciare
Prendiamo il caso di tracciare la funzione x2 +y2 per i valori di x e y nella porzione di piano [-1...1,-1...1]
>> x=linspace(-1,1,100); y = x; >> [xx,yy]=meshgrid(x,y);
Usiamo quindi l'operatore di prodotto elemento per elemento di 2 matrici e calcoliamo il valore della superficie (asse z )
>> z=(xx.*xx + yy.*yy);
Infine combiniamo tra loro queste matrici per tracciare la superficie
>> mesh(xx,yy,z)
Oppure
>> surf(xx,yy,z)
$$ e^{\frac{-(x^2+y^2)}{d}} \cdot cos(2 \pi \omega \cdot (x^2+y^2))$$
assegnando a omega e d valori di volta in volta diversi (suggerimento: partite con i valori omega=2 e d=0.5 per poi cambiarli). Prestate attenzione al significato e alla rappresentazione degli elementi e operazioni che compaiono nell'espressione data. Il risultato dovrebbe essere come quello raffigurato qui a fianco. E' in generale utile esaminare separatamente le due funzioni che vengono moltiplicate tra loro e comunque è importante:- Prestare attenzione alla priorità degli operatori
- Nel caso si debba modificare la priorità degli operatori e
raggruppare tra loro termini si deve osservare il bilanciamento delle parentesi.
Comunque sia il numero di parentesi
aperte
deve sempre essere uguali alle parentesichiuse
presenti nell'espressione. - Considerare se una funzione o operatore si applica elemento per elemento
- Se ci sono espressioni ricorrenti o speciali è utile calcolarle separatemente e memorizzarle in una matrice separata. In questo caso può essere utile salvare in una matrice l'espressione \(x^2+y^2\) che appare in 2 punti. Questo aiuta a ridurre gli errori e rende i comandi più leggibili
Cambiando i valori di d
e omega
cambiano il numero
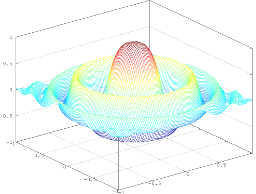 sombrero.png
di oscillazioni e la loro distribuzione. E' importante notare il rapporto tra il
valore dei parametri che controllano la superficie e il dominio della superficie
le cui coordinate sono memorizzate nelle matrici xx
e yy
. Si può
cambiare la dimensione della matrice aumentando il numero di righe e colonne variando
il valore del terzo parametro della funzione linspace
: la matrice avrà una
dimensione diversa, ma l'output manterrà lo stesso aspetto
sombrero.png
di oscillazioni e la loro distribuzione. E' importante notare il rapporto tra il
valore dei parametri che controllano la superficie e il dominio della superficie
le cui coordinate sono memorizzate nelle matrici xx
e yy
. Si può
cambiare la dimensione della matrice aumentando il numero di righe e colonne variando
il valore del terzo parametro della funzione linspace
: la matrice avrà una
dimensione diversa, ma l'output manterrà lo stesso aspetto
Plot di una superficie come immagine
Suppomiamo di memorizzare la superficie nella variabile zz
.
Un'immagine a scala di grigi è rappresentabile come superficie e viceversa. Una volta
osservato l'aspetto della superficie di prova dovrebbe essere naturale intepretare
l'output del comando
imshow
 applicato alla matrice zz
.
Prima di tutto però questa matrice va riadattata in modo che
i valori contenuti possano essere interpretati come un'immagine grayscale
. Per
praticità prendiamo un'immagine a scala di grigi come una distribuzione bidimensionale
di valori compresi nell'intervallo [0,1]
. Octave offre la funzione
mat2gray
che converte una matrice data in una nuova matrice i cui valori sono compresi tra 0 e 1
(se non viene specificato un intevallo tramite il secondo argomento),
fissando a zero il valore minimo della matrice ad uno il valore massimo e calcolando i
nuovi valori intermedi mantenendo la proporzionalità delle differenze rispetto al minimo.
applicato alla matrice zz
.
Prima di tutto però questa matrice va riadattata in modo che
i valori contenuti possano essere interpretati come un'immagine grayscale
. Per
praticità prendiamo un'immagine a scala di grigi come una distribuzione bidimensionale
di valori compresi nell'intervallo [0,1]
. Octave offre la funzione
mat2gray
che converte una matrice data in una nuova matrice i cui valori sono compresi tra 0 e 1
(se non viene specificato un intevallo tramite il secondo argomento),
fissando a zero il valore minimo della matrice ad uno il valore massimo e calcolando i
nuovi valori intermedi mantenendo la proporzionalità delle differenze rispetto al minimo.
I valori minimo e massimo nella matrice zz sono
>> min(min(zz)) ans = -0.61422 >> max(max(zz)) ans = 0.99959
Una volta convertita in un'immagine grayscale
>> zz=mat2gray(zz); >> min(min(zz)) ans = 0 >> max(max(zz)) ans = 1
